Alasdair’s Engineering Pages © A. N. Beal 2024             www.anbeal.co.uk

www.anbeal.co.uk

The Structural Engineer, Vol. 82 No. 22, 16th November 2004

A bit windy? Anomalies in BS 6399-2

A N Beal BSc CEng MICE FIStructE

Alasdair Beal (F) argues that several aspects of the new wind code are open to different interpretations and suggests a way forward

One only needs to go back to R. G. Taylor’s wonderfully-entitled ‘Blow, blow thou winter wind, th’art not so unkind as CP3 Chapter V: Part 2 1972’ [1] to realise that BS 6399-2 [2] is not the first new wind code to attract controversy. In the 7 years since it first appeared, there have been heated debates in The Structural Engineer, Digests from the BRE [3] and an SCI/BRE/BCSA Guide to help engineers to use it [4] but, despite all this effort, BS 6399-2 is still a deeply unpopular code. Initially it was hoped that this came from unfamiliarity but experience in practice suggests that the Code has some more deeply-rooted problems. Some examples are outlined below, together with suggestions for improvements (all are based on the BS 6399-2 Standard Method).

Complexity

Even in this computer age, simplicity in calculations is still a virtue: over-complicated calculations mean higher design costs, more mistakes - and, as the engineering vision becomes lost in the mathematical analysis, cruder and less elegant designs.

BS 6399-2 tends to present information about different aspects of wind behaviour in a ‘pure’ form, leaving the engineer to combine the various elements in the calculation process. Although this is admirable from a theoretical point of view, it means that the design implications of a code requirement may not be clear until several separate calculations have been completed and the results combined.

There are also rules which appear  simple in the Code but generate surprising complexity in practice. For example, for external wind pressures BS 6399-2 replaces CP3 Chap. V’s exposure classes ‘A’ ‘B’ and ‘C’ with a single ‘size effect factor’ Ca based on the diagonal dimension a of the area loaded by a wind gust. This appears very simple but in practice every element in a building can have a different a and hence a different factor.

Furthermore, for a pitched roof BS 6399-2 replaces CP3-V’s eight external pressure coefficient zones with ten and it replaces CP3-V’s two internal pressure coefficients (+0.2/-0.3) with maximum and minimum pressures which may be different for every room in the building (Cl. 2.6.1.2 - depends on room size).

These may seem like minor gripes. However consider the roof of a typical shed with (say) four different-sized rooms inside. CP3-V would give eight zones of external pressure, each with a Class ‘A’ value for cladding and fixings and a value which would be either ‘Class B’ or ‘C’ for the structure: 16 different external pressures, to combine with two possible internal pressures, giving 32 possible combined pressures for design. BS 6399-2 has 10 external pressure zones and the cladding, purlins and beams can each have one or more different pressures (based on a value), so there are at least 30 different external pressures; maximum and minimum internal pressures will be different for each of the four rooms, so in total there will be at least 30 x 2 x 4 = 240 possible different combined wind pressures. (If some beams and purlins support different loaded areas, there could easily be over 1000 different design wind pressures.)

Even if the engineer had the time to work out all these different wind pressures and to design all the possible variations of cladding fixings, purlin sizes, connection details etc. to take full advantage of them, the proliferation of different section sizes and details would make the structure hopelessly uneconomic and impractical to build. Modern commercial design relies on rationalisation and repetition of sections and details to achieve maximum economy - and this means design wind pressures must also be rationalised. Engineers can either calculate all the different possible combined pressures generated by BS 6399-2 and then rationalise them into a limited set of values for design, or else they can simply base their calculation of design pressures on a limited range of ‘worst case’ assumptions. Either way, once the necessary simplifications and rationalisations have been made to achieve a practical design, the results may be quite crude and conservative, making all the complex calculations difficult to justify. For normal commercial work, a simpler approach is needed which generates fewer permutations and enables engineers to work out sensible design wind pressures more quickly and easily.

The main cause of the proliferation of design wind pressure values is the ‘size effect factor’ Ca. It can generate a different internal pressure for every room size (see later) and the values for external pressures are presented on a large-scale graph (BS 6399-2 Fig. 4), plotted in increments of 0.01 for all values of from 0 to 1000m, with finely-tuned adjustments for height of building, distance from the sea etc. However is this level of precision really necessary (or even valid) when estimating the design wind loads on an ordinary building? (Variations in pressure coefficients are generally quoted only in increments of 0.1.)

It is worth remembering that the practical range of variation of Ca is actually quite small: over the realistic range of building sizes, it almost always falls in the range 0.75-1.0. Therefore BS 6399-2 Fig 4 could be greatly simplified with little loss of accuracy. Table 1 below shows how this could be done. For normal purposes Ca can be taken as constant for the range of a dimensions above each value quoted (i.e. 5-10m/10-20m/20-50m/50- l00m). However interpolation may be used where ‘fine tuning’ is required.

(For a building in town at least 10km from the sea and He ≤ l0m, or in town 2-10km from the sea and He ≤ 5m, values in brackets 0 may be used.)

 

 

 

 

 

 

Size matters - calculating ‘a’

BS 6399-2 defines a as ‘the largest diagonal of the area over which load sharing takes place’ (Cl. 2.1.3.4). It gives illustrations of this for panels or faces of buildings but there are no diagrams showing a for an individual beam or column. BRE Digest 436 (Q18) and the SCl/BRE Guide [4] suggest that a should be taken as the diagonal dimension of the ‘tributary area’ loading the beam. The SCI/BRE Guide proposes (p. 41) that for continuous beams, this ‘tributary area’ can be taken as extending across two beam spans.

It can easily be demonstrated that neither of these is correct. A ‘tributary area’ is a convenient calculation shortcut but it is not the same as the area contributing load to the beam. Fig 1a shows influence lines for the reaction on a beam. As can be seen, the area which contributes load to the beam when it is loaded for maximum reaction is always wider than the ‘tributary area’: for an individual beam, the loaded area extends across the full panel width on each side of the beam and for flexible beams with some load-sharing it extends across at least two panels on each side (Fig 1b). These are the loaded areas which should be used for determining wind loads, rather than the smaller ‘tributary areas’ (see Figs 2a and 2b).

Fig. 1a
Influence line for reaction at central support of continuous beam

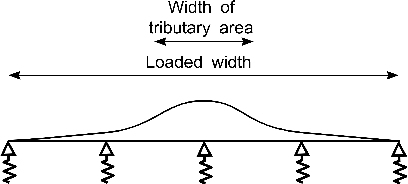
Fig 1b
Influence line for reaction at central support of continuous beam on flexible supports

Fig. 2a
Loaded area for calculation of a: stiff beams, no loadsharing

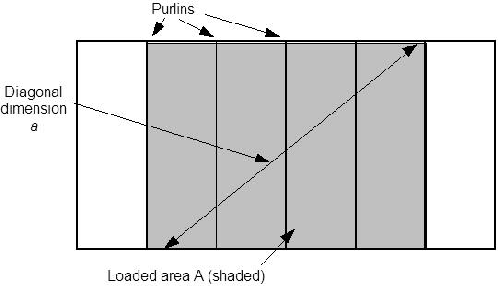
Fig. 2b
Loaded area for calculation of a: flexible beams with loadsharing

The SCI/BRE proposal to base a for double-span purlins on twice the purlin span is arguably correct if the purlin design is governed by the elastic value of the support hogging moment. However in all other cases, e.g. plastic design, or where the midspan moment governs the design, single span loading is critical and design based on the SCI/BRE proposal would be wrong.

Multibay pitched roofs

Many industrial sheds have multibay pitched roofs and wind uplift is critical for the design of their roof sheeting, its fixings, the purlins and the roof beams or trusses. CP3 Chap. V Table 11 gave wind pressure coefficients for multibay roofs. However BS 6399-2 does not. It considers only single bay roofs (either central valley or central ridge) in detail (Table 10). To calculate pressures on a multibay roof, a series of these ‘toy houses’ must be placed side by side and then rules in Cl. 2.5.5 followed to adjust the results. Unfortunately this only considers conditions with the wind blowing perpendicular to the ridges and says nothing about the pressures caused by wind blowing parallel to the ridges, even though the latter can be critical for uplift pressure on large areas of the roof.

Is an internal bay of a multibay roof:

(i) part of a series of troughed roofs (negative pitch)? or

(ii) part of a series of ridged roofs (positive pitch)?

If (i) is correct BS 6399 Table 10 gives a suction coefficient of -0.8 (Fig 3a) for zone C of a 15° pitch roof. However if (ii) is correct, the coefficient is -0.6 (Fig 3b). For a roof pitch of 30°, the coefficient can be either -1.0 or -0.6. Which is correct? The Code does not say. This is a serious anomaly, which clearly needs to be sorted out.

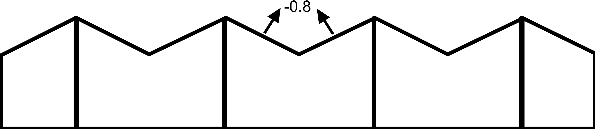
Fig 3a. Cpe -15° pitch roof, (BS 6399-2, Table 10)

Fig 3b. Cpe +15° pitch roof, (BS 6399-2, Table 10)

The ‘penthouse problem’

BS 6399-2 Clause 2.4.4.2 gives design pressures for walls of inset top storeys. Whilst these may be sensible in some circumstances, the recommendations can have severe effects on the top storeys of a multistorey building.

If the walls of the building extend flush-faced right to the top, the maximum suction coefficient for the cladding (Zone A) is generally -1.3. However if the sides of the top storey are inset (even only slightly), some of its side cladding must be designed for a suction coefficient of -2.0 (Fig 15(b) Zone E). On a multistorey building it is very common for the walls of the top one or two storeys to be inset slightly relative to those below, either as an architectural feature or to form a penthouse balcony. The walls of these areas have generally been relatively trouble-free and it is difficult to believe that insetting the wall line at this level in this way could generate such a dramatic increase in wind pressures.

An odd feature of this clause is that this 50% pressure increase appears to apply regardless of whether the inset of the upper walls is 0.3m or 30m and regardless of whether the inset is at low level or near the top of the building. Is there something wrong with the scaling rules in this clause, which adjust its effects for varying proportions of buildings?

Internal pressures

Internal pressures are normally thought of as rather mundane but they form an important part of the loading on many structural elements. They are difficult to calculate precisely, so engineers using CP3 Chapter V were usually content to follow its recommendation (Appendix E) that:

‘Where it is not possible, or is not considered justified, to estimate the value of Cpi, for a particular case, .... where there is only a negligible probability of a dominant opening occurring during a severe storm, Cpi should be taken as the more onerous of +0.2 and -0.3’.

BS 6399-2 Cl. 2.6.1.1 says much less than CP3 Chapter V Appendix E and its Table 16 only gives internal pressure coefficients for two types of building:

(i) two opposite walls equally permeable, other faces impermeable: internal pressure coefficient -0.3/+0.2 (depending on wind direction) and

(ii) four walls equally permeable, roof impermeable: internal pressure coefficient -0.3.

These coefficients are then multiplied by coefficient Ca with a = 10 ³√(internal volume of storey).

No advice is given for any other types of building. There is also another problem: what exactly does (ii) mean? Is the internal coefficient - 0.3 constant in all situations, or is it a maximum value, with the alternative of 0 also to be considered? The BRE Digest (Q. 43) and the BRE/SCI Guide (p. 44) both say that for completely clad warehouse-type buildings, Cpi may be taken as a constant -0.3 but BS 6399-2 itself gives no clear guidance on the matter. Many engineers will play safe and design for -0.3/0. However there are other issues to consider before reaching a conclusion.

“... and I’d like to have a partition here”

Where there are internal walls with internal doors which are either kept open, or else more than three times more permeable than the external doors, BS 6399-2 Clause 2.6.1.1 states that internal wind pressure may be taken as uniform. For other cases, Cl. 2.6.1.2 states that lateral pressure on internal walls must be considered (coefficient 0.5) and external walls enclosing a room should be designed for internal pressure coefficients +0.2/-0.3. Although Cl. 2.6.1.2 does not specifically mention roofs, presumably the roof over a room is subject to the same internal pressures as its walls. This means that in a shed with no internal partitions the external walls and roof may be designed for an internal pressure coefficient of either -0.3 or -0.3/0 (depending on how BS 6399-2 Table 16 is interpreted). However if the shed has internal partitions, a coefficient of +0.2 must also be considered.

Consider a shed measuring 50m (L) x 25m (B) x 12m (H) with a dynamic wind pressure of 1kN/m², designed in accordance with the BRE/SCI guide. If the roof external pressure coefficient is -0.6 and Ca for the purlins is 0.96, the external pressure on the roof is -0.58kN/m². If the internal pressure coefficient is taken as -0.3, a = 247, Ca = 0.70 and the internal pressure is -0.21kN/m², so the net wind uplift for purlin design of  0,37kN/m². However if the shed is divided by an internal wall, an internal pressure coefficient of +0.2 must be considered; in this case, a = 196, Ca = 0.72 and the internal pressure is +0.14 kN/m², giving a net wind uplift of 0.72kN/m². Thus simply constructing a partition wall inside the shed would almost double the calculated uplift pressure on its roof.

At some point in the life of almost every building, someone will erect walls inside it, perhaps to divide the space, or for office areas, or for subletting. If the design does not allow for this, owners and tenants will need to be notified that they cannot erect internal partitions without first strengthening the roof fixings and supports. This would also need to be recorded in the CDM Health & Safety Plan and sale and letting particulars - and maybe there should be permanent warning notices. However is it reasonable and realistic to design a normal commercial building on this basis?

Is internal pressure constant?

When the wind blows past a building, more wall areas have negative external pressure coefficients than positive, so if all the walls are equally permeable it is reasonable to assume that the air pressure inside the building will be reduced. However is it reasonable to assume that this reduction is constant for all wall permeabilities?

Consider a building with four walls of exactly equal permeability and an impermeable roof Imagine what happens if the permeability of the all walls is progressively reduced. We know that if the walls are completely impermeable, the wind outside will have no effect on the air pressure inside, so Cpi must be 0.0. It is reasonable to deduce from this that as the wall permeability is reduced towards zero, the internal pressure change induced by the wind must also reduce towards zero. A lot of research would be necessary to work out the full relationship between wall permeability and internal wind pressure (particularly when wall permeabilities are not exactly equal) but this simple ‘thought experiment’ is sufficient to establish two important points:

i) the internal pressure cannot be a constant proportion of the external wind dynamic pressure for all wall permeabilities and

ii) where the wall permeability is low, it cannot be correct to assume that the internal pressure coefficient is always -0.3, as recommended by the BRE Digests and the SCI/BRE Guide: values approaching 0.0 must also be possible.

‘All walls equally permeable’?

How valid is it to design real buildings on the assumption of ‘four walls equally permeable’? BRE Digest 436 (Q 43) states that the definitions of ‘permeable’ and ‘impermeable’ are relative and may be distinguished by a factor of 2. It also acknowledges that ‘In general, faces with opening windows and doors or ventilators will be permeable and faces without openings (masonry, profiled metal cladding etc.) will be impermeable’ - but then goes on to propose that ‘the internal pressure coefficient for completely clad enclosed warehouse-type buildings, without opening windows, may be taken as Cpi = -0.3’.

Very few real buildings have (even nominally) ‘four walls equally permeable’. The side walls are often fairly impermeable but the rear wall usually has at least one door or window and the front wall almost always has one or more doors and one or more windows; roofs and walls also commonly have air vents. Then there are the vagaries of real construction: at the design stage the actual permeabilities of walls are rarely known to any accuracy and even for nominally identical construction the real permeability may vary considerably in practice. Finally, wear and tear and also building alterations should be considered: flues and extractor fans may be installed and new door and window openings may be formed. All these things may play havoc with calculations based on idealised assumptions - and it is simply unrealistic for a designer to assume that they will not happen. It only needs one wall to become more than twice as permeable (or less than half as permeable) as the rest and suddenly an internal pressure of +0.2 must be considered, according to BS 6399-2 Table 16.

Recommended internal pressures for design

When all of the above is taken into account, it is difficult to see how the idea of designing standard commercial sheds for a constant internal pressure coefficient of -0.3 can be sustained, either theoretically or practically. At the very least, the alternative of 0.0 should also be considered but, unless building owners are prepared to accept bans on erecting internal partitions or creating or infilling openings in external walls, it is hard to escape the conclusion that engineers should also allow for an internal pressure coefficient of +0.2.

It should be noted that BS 6399-2 reduces internal pressure coefficients by the size effect coefficient Ca. In theory this should be varied for the size of every room (or possible room) but in practice Ca rarely falls outside the range 0.65-0.90, so the range of possible internal pressure coefficients is (-0.2 to -0.27)/(+0.13 to +0.18). For normal purposes, it would be reasonable to drop Ca from the calculation and adopt constant Cpi values of- 0.25/+0.15.

Dominant openings

In BS 6399 Cl. 2.6.2 the internal pressure when a dominant opening is open in a storm is superficially similar to CP3 Chapter V: depending on its size, it is based on either 75% or 90% of the pressure outside the opening. However, because of differences in the way the pressure is calculated, the results are quite different from CP3.

In CP3, normal practice (rightly or wrongly) was to base the external wind pressure at the dominant opening (and thus the internal pressure) on:

(a) exposure class based on overall dimensions of the building (e.g. Class 3B or 3C) and

(b) wind pressure coefficient based on height of top of door opening.

In BS 6399, the pressure caused by the dominant opening is based on:

(a) external pressure based on the height of the top of the building and

(b) the size effect factor Ca based on the diagonal dimension a of the opening, or the volume of the room or building storey containing the opening (a = 0.2x ³√(internal volume of storey)), whichever is greater.

The practical effect of the CP3-V recommendations was that increasing the size of the opening increased the internal pressure. In BS 6399, where doorway size governs, increasing the size of the opening reduces the internal pressure.

To determine whether an opening is ‘dominant’, BS 6399-2 Table 17 requires the engineer to calculate the ratio between the dominant opening and the ‘sum of remaining openings and distributed porosities’ - but it gives no guidance on the latter and few engineers will have the necessary information to hand. BRE Digest 436 acknowledges (Q 44) that ‘There is little information available on absolute values of porosity’ but it suggests typical values for some forms of construction (which unfortunately do not include standard industrial shed cladding).

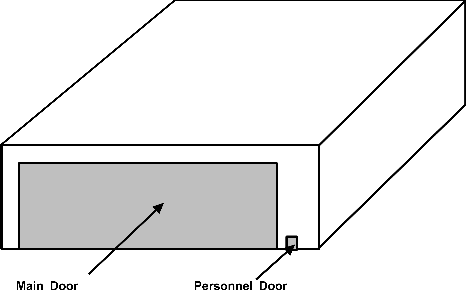
Fig. 4
Dominant openings

Consider a hangar on a site in the country measuring 50m (L) x 50m (B) x 18m (H), with two doorways in its front wall: a main door 40m wide x 15m high and a smaller personnel door 1.5m wide x 2. lm high (Fig 4). Assume that the design external wind pressure on the front wall is 1kN/m².

Firstly the ‘sum of remaining openings and distributed porosities’ on the side and rear walls must be calculated. Their area is 2700m² and if their porosity is taken as similar to office curtain walling (3.5 x 10-4 according to Digest 436), they have a total opening area of 2700 x 3.5 x 10-4 = 0.95m². The main doorway and the small personnel doorway are both at least three times this so, according Table 17, they are both potential dominant openings with Cpi = 0.9. The value of a based on

(i) building volume = 0.2³√(internal volume) = 7. 1m, giving Ca = 0.98;

(ii) for the main doorway, a = 42.7m and Ca =0.84;

(iii) for the personnel doorway, a = 2.6m and Ca = 1.00.

If the main doors are left open in a storm, (ii) governs, so the internal pressure = 0.9 x 0.84 x 1kN/m² = 0.76kN/m². However if the personnel door is left open, (i) governs and internal pressure = 0.9 x 0.98 x 1kN/m²  = 0.88kN/m².

Therefore, according to BS 6399-2, the worst pressure inside the building is not caused by leaving the main doors wide open in a storm - it occurs when the small personnel door is left open, which creates 15% greater internal pressure. Both common sense and basic considerations of airflow suggest that this is wrong.

The problem appears to arise because Ca  is based on the diagonal dimension of the doorway, which gives the average pressure on the door when it is shut - and the average wind pressure on a small closed door can be greater than on a large door. However when a door is open, the wind pressure created inside the building depends on the airflow through the open doorway; less air will flow through a small opening than through a large one, so the smaller opening should create a smaller internal pressure. This part of BS 6399-2 needs to be revised.

Probability and serviceability

BS 6399-2 Cl. 2.6.1.3 states that ‘Where an external opening, such as a door, would be dominant when open but is considered to be closed in the ultimate limit state, the condition with door open should be considered as a serviceability limit state’.

What does this mean? A ‘serviceability limit state’ is normally a limit on cracking, deflexion etc. and in most cases it is impossible to satisfy this without also satisfying the ‘ultimate limit state’. However if this was the intended meaning, Cl. 2.6.1.3 would make no sense at all. What did the BS 6399-2 committee have in mind? There have been various interpretations of this curious clause.

The SCI Guide proposes (p. 48) that the Cl. 2.6.1.3 ‘serviceability limit state’ should be considered as equivalent to an accidental limit state, checking the design against failure using a load factor of 1.0. However this contradicts everything said on the subject of limit state design in BS 8110, BS 5950 and BS 5628, which define completely different performance criteria for ‘serviceability limit states’ and ‘accidental limit states’. BS 6399-2 itself says nothing which would support the SCI Guide proposal either. The idea is probably best discounted.

BRE Digest 436 Part 1 (Q 46) suggests checking the ‘serviceability limit’ at a reduced wind speed, with Sp = 0.8 applied to the characteristic wind speed, reducing the design dynamic pressure to 64% of the characteristic value; this is said to correspond to ‘a return period of 2 years’. The SCI Guide makes a similar suggestion but describes the loading probability as ‘a mean recurrence interval of 1.8 years’. However BS 6399-2 Annex D does not agree with either of these: it says that Sp for ‘the serviceability limit’ is 0.845, the design wind pressure is 71% of the characteristic value and the probability of occurrence is 0.227 (1/4.5) per year. It seems clear that whatever BS 6399-2 Cl. 2.6.1.3 means, it does not mean what either the BRE Digest or the SCI Guide say it means.

However the strange affair of Cl. 2.6.1.3 does not end here. What is the origin of that curiously-precise value of S = 0.845? Annex D Note 2 says: ‘For the serviceability limit, assuming the partial factor for loads for the ultimate limit is γf = 1.4 and for the serviceability limit is γf  = 1.0, giving Sp = √(1/1.4) = 0.845’.

This analysis contains two major errors.

(i) The partial factors on loads used in ultimate limit state design are safety factors, not estimates of real loads. The values in present UK limit state codes were selected on a fairly arbitrary basis by the CP110 committee in the early 1970s and have stayed more or less unchanged since then. They have no rigorous scientific or technical basis and they tell us nothing useful about wind loadings.

(ii) If a code says that γf = 1.4 for the ‘ultimate’ load and γf = 1.0 for the ‘serviceability’ load, this means ultimate load = 1.4 x characteristic load and serviceability load = 1.0 x characteristic load. It does not mean serviceability load = 1.0/1.4 x characteristic load.

Despite its apparent precision, the derivation of Sp in BS 6399-2 seems to have no rational basis and it appears to be based on a complete misunderstanding of partial factor/limit state theory. There is nothing wrong in principle with the idea of designing for a reduced wind speed where a dominant opening is unlikely to be left open in a storm. However in its present form this section of BS 6399-2 is confusing and illogical - and the BRE Digest and BRE/SCI Guide only compound the confusion and errors.

Conclusions

* When calculating Ca  for a beam or column, the diagonal dimension a should be based on a loaded area of the full panel width on each side of the beam, not the smaller ‘tributary area’ recommended by the BRE Digest and the BRE/SCI Guide. Where a beam is flexible and may share load, a loaded area of two panel widths on each side may be taken (see figs. 2a and 2b).

* The size effect factor Ca, for external pressures could be simplified with little loss of accuracy, greatly reducing the number of different wind pressures generated for design (see Table 1).

* The BS 6399-2 recommendations for wind pressure on a multibay roof do not consider wind parallel to the ridges properly and contain major anomalies. A separate, properly worked-out table of pressure coefficients for multibay roofs is needed (as was done in CP3-V).

* The rules for wind pressures on walls of buildings with inset upper storeys appear to give odd and very onerous results in some situations.

* The BS 6399-2 guidance on internal pressures is inadequate. For both theoretical and practical reasons it is not appropriate to design normal commercial buildings for a constant internal pressure coefficient of Cpi = -0.3 (as recommended in the BRE Digest and SCI/BRE Guide). The alternative of Cpi = +0.2 should also be considered.

* The calculation of internal pressures could be simplified by incorporating Ca into Cpi, giving coefficients of -0.25/0.15 for normal design.

* The BS 6399-2 treatment of internal pressure created by a dominant opening in a storm gives illogical results. The effects of varying opening size need to be treated in a more believable way.

* Where a dominant opening is unlikely to be open in a storm, it is reasonable to use a reduced wind speed for estimates of internal pressure. However the BS 6399-2 description of this as a ‘serviceability’ condition is confusing and misleading and the derivation of Sb in Annex D contains major errors. The SCI/BRE Guide proposal that ‘serviceability’ can be equated with ‘accidental’ loading appears to have no justification.

Acknowledgments

Thanks are due to my colleagues Adam Nycz and David Hart for their help in identifying the problems discussed in this paper.

References

1. ‘Blow, blow thou winter wind, th’art not so unkind as CP3 Chap. V Part 2’, Taylor, R. C., The Structural Engineer, V 51/12, Dec. 1973 and discussion V 52/9, Sept. 1974, IStructE, London.

2. BS 6399-2:1997: ‘Loading for Buildings: Code of practice for wind loads’, BSI, London, 1997.

3. BRE Digest 43: ‘Wind loading on buildings: brief guidance for using BS 6399-2:1997’, BRE, Garston, 1999

4. SCI Publication: ‘Guide to evaluating design wind loads to BS 6399-2:1997’, p. 286; SCI, Ascot, in association with BRE and BCSA, 2003.

<< Return to top

Table 1: Proposed table of size effect factor Ca for external pressures