Alasdair’s Engineering Pages © A. N. Beal 2024             www.anbeal.co.uk

www.anbeal.co.uk

The Structural Engineer, Vol. 70, No. 23/24, 8 Dec. 1992

Simple design of multibar concrete columns

A. N. Beal BSc CEng MIStructE MICE (Thomason Partnership)

F. N. Pannell BSc MSTech PhD CEng MlStructE

Introduction

Reinforced concrete columns are now often designed by computer but design charts are still a popular alternative. Many sets of charts have been published for different Codes of Practice over the years, by various authors, but most of those for rectangular columns (e.g. BS8110:Part 3 [1]and the IStructE manual [2]) cover only columns that are reinforced with four bars placed near their corners.

While this is probably the most common bar arrangement, many columns in practice -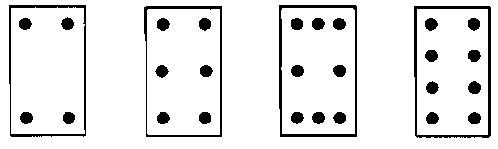 particularly the larger sizes - may have six, eight or more bars placed in a variety of arrangements (Fig. 1). As most columns are subjected to a degree of biaxial bending, it is therefore often necessary to design reinforcement or assess the resistance moment for one of these less efficient arrangements.

Fig. 1 Common bar arrangements in RC columns

Pannell [3] published comprehensive charts for the design of multibar columns to CPI14. These are effective but rather laborious to use; for accurate design they have been effectively superseded by the use of computer programs. However a full rigorous analysis is not always wanted and there is a need for a simple, approximate method of design.

The IStructE manual gives an approximate method for multibar columns: any bars in the side faces of the column are simply ignored and only the outer bars are considered in the analysis. Fig. 2 shows the comparison between rigorous BS 8110 analysis and this approximate method for a six-bar column with d = 0.85h. The approximate method is simple and always errs on the safe side but, as can be seen, the result can be very conservative when the axial force is high and the moment is low.

The BS8110 handbook [4] suggests an alternative method: for calculation purposes the six, eight or more bars in the column are replaced by four bars of equivalent total area, placed at the centroid of the group of bars on each side of the neutral axis. This avoids the conservatism of the ‘green book’ method when moments are low, giving clearly better results (see Fig.  2), However, the method is still conservative and six bar columns with d of less than 0.875h (equivalent four-bar effective depth d = 0.75h) cannot be analysed using the BS8110 charts, which do not extend to below d = 0.75h.

Fig 2. ‘Green book’ and BS8110 handbook approximate analysis compared with exact analysis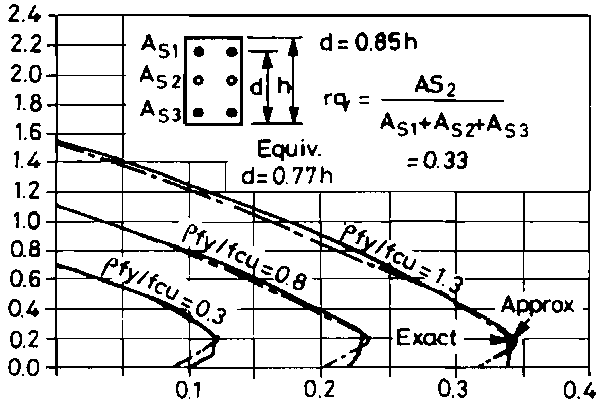

Fig 3. Proposed approximate analysis

As can be seen from Fig. 2, for a six-bar column with ρfy/fcu = 0.8 the ‘green book’ method underestimates axial load capacity by  almost 20%  and the peak moment capacity by 7%. The BS 8110 handbook method is clearly best for most situations - but still the peak resistance moment is underestimated by 14%.

During preparation of the IStructE publication Recommendations for the permissible stress design of reinforced concrete structures [5] (the ‘gold book’) the need for simple, accurate design charts capable of covering most practical situations was felt to be important. This led to the development of the method outlined here.

Proposed method

In order to refine the ‘equivalent effective depth’ method a comprehensive analysis of BS 8110 rectangular multibar columns was carried out across the whole range of reinforcement coefficients (ρfy/fcu) 0.2 to 1.4 and the range of ratios of side bars to outer bars (rq) 0.2 to 0.8. In the calculations, three layers of steel were assumed for rq = 0.0 to 0.4 and five layers of steel were assumed for rq  over these values.

Fig. 3 shows the detailed comparison between exact analysis and the proposed simple method for the six-bar column referred to earlier (d = 0.85h, rq = 0.33). The equivalent ‘four- bar’ effective depth is 0.77h and Fig. 3 compares results based on this for steel coefficients (ρfy/fcu) of 0.3, 0.8, and 1.3. As can be seen, the agreement is very close indeed; the approximate method gives answers which are accurate enough for most ordinary purposes. Similarly good agreement was obtained across the whole range of columns analysed.

Table 1 summarises the results of the analysis. In all, a total of 140 different arrangements and proportions of column reinforcement were analysed across the full range of axial loads and moments, and the results were compared with the equivalent four-bar column curves.

As can be seen, for each ratio of side bars rq the equivalent effective depth is virtually constant across the full range of reinforcement proportions and for design purposes the results can be reduced into a single table. This is given in Table 2 and Fig 4 shows the results in graphical form for convenience. This allows standard four-bar column curves to be used for the design of multibar columns and gives good accuracy. It is considerably more economical than the ‘green book’ method.

When compared with the BS 8110 handbook method, the more exact figures for equivalent effective depth give an extra degree of economy but also, perhaps more importantly, they allow the standard four-bar charts to be applied to multibar columns with a wider range of effective depths - e.g. BS 8110 standard charts can now be used to design six-bar columns with effective depth down to d = 0.82h, compared with a limit of d = 0.875h for the BS 8110 handbook method. This brings a larger range of real multibar columns within the range of simple design based on the standard charts.

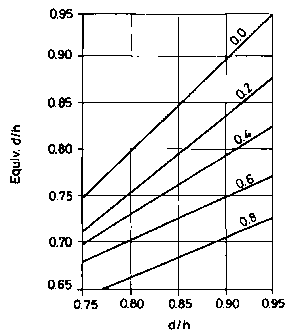
Fig 4.
BS8110: equivalent effective depths

Permissible stress design

As noted earlier, the proposed method was first developed for the IStructE publication [5]. A full analysis was again made across the whole range of reinforcement arrangements, axial forces, and moments. Again the comparison between rigorous analysis and the ‘equivalent effective depth’ four-bar curves produced good agreement, similar to that demonstrated above for BS 8110. The appropriate values of equivalent effective depth are tabulated and also shown in graphical form (Table 3, Fig. 5). In the ‘gold book’, four-bar column charts are provided for effective depths down to d = 0.7h, so the method allows, for example, six-bar columns with d as low as 0.75h to be designed, which covers almost the whole practical range.

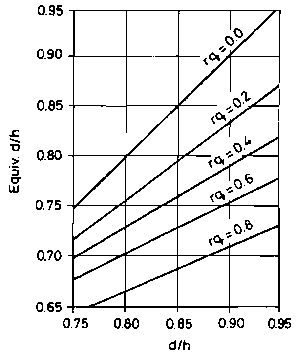
Fig 5.
Permissible stress design:
equivalent effective depths

Conclusions

Multibar rectangular concrete columns can be designed using the published curves for four-bar columns if the effective depth of the multibar column is transformed into an equivalent four-bar effective depth. The coefficients vary with the proportion of steel placed in the sides of the section. The method gives ample accuracy for most normal design, making more elaborate analysis unnecessary. The method can be used with either limit state or permissible stress design Codes and provides a simple, more accurate alternative to the approximate method suggested in the IStructE manual (the ‘green book’). It is also more accurate and more widely applicable than the approximate method proposed in the BS 8110 handbook.

References

1.  BS 8110 Structural use of concrete: Part 3, London, British Standards Institution, 1985.

2.  IStructE/ICE Manual for the design of reinforced concrete building structures, London, Institution of Structural Engineers, 1985.

3.  Pannell, F. N.: Design charts for members subjected to biaxial bending and thrust, London, Concrete Publications Ltd

4.  Rowe, R. E., et al: Handbook to British Standard BS8110, Palladian Pubs Ltd, London, 1987, p. 64.

5.  Recommendations for the permissible stress design of reinforced concrete building structures, London, Institution of Structural Engineers, 1991.

<< Return to top

TABLE 1 - Effective depth shifts for steel in side faces (design to BS 8110) (rq = side steel/total steel)

TABLE 2 - Equivalent effective depths for design to BS 8110
(rq = side steel/total steel)

TABLE 3 - Equivalent depths for permissible stress design
(rq = side steel/total steel)