Alasdair’s Engineering Pages © A. N. Beal 2024             www.anbeal.co.uk

www.anbeal.co.uk

Concrete February 2010

Fabric-reinforced concrete ground slabs and Concrete Society Technical Report TR34/3

Alasdair N Beal, Thomasons

In 2003, the Third Edition of Concrete Society Technical Report 34 [1] was published. It brought together guidance for all types of industrial ground slab in one publication and also introduced a new design method for fabric-reinforced ground-bearing slabs. This article reviews results obtained by the new method and compares these with the results of past practice.

For many years, the UK ‘Bible’ for designing concrete ground-bearing slabs was Colin Deacon’s Concrete Ground Floors: their design, construction and finish [2]. Chandler’s TR550 Design of Floors on Ground [3], gave additional guidance on calculating slab thickness and was later refined by BCA Interim Technical Note [4], which introduced standard design loading categories.

The first and second editions of Concrete Society Technical Report 34 (1988, 1994) relied on TR550 for design of fabric-reinforced ground-bearing slabs but the Third Edition introduced a new, completely different design method.

* TR550 uses elastic analysis of slab bending capacity, whereas TR34/3 uses plastic analysis.

* According to TR550, ‘a sub-base reduces the stress induced in the slab and, in the case of wheel and rack loads, assists in the distribution of the load to the sub-grade’ (p.6) and ITN 11, Table 1 gives enhanced subgrade properties for increased sub-base thickness. However, TR34/3 takes the opposite view: ‘Any enhancement of the modulus of subgrade reaction produced by a compacted granular sub-base is so small that, compared with the variations in properties that will occur in a natural soil, it should be neglected in the design process’ (6.4.1, p.35).

* In TR550 the safety factor on dynamic loads varies depending on number of load repetitions, to prevent fatigue failure, whereas in TR34/3 it is constant (9.6.3, p.54).

* In TR550 (p.9), assumed load transfer across a joint is 15% (single joint) or 30% (joint intersection). In TR34/3, it can be up to 50%.

Comparison

The following analysis compares TR34/3 and TR550/ ITN 11 for a slab supporting ‘Category 2’ (Medium) loading, with 3t forklifts (3.75-tonne wheel load, solid tyres) and 3-tonne racking legs (300mm c/c, 150mm from slab joint). Concrete cube strength is 40MPa, A142 fabric reinforcement (50mm bottom cover) and it is laid on 150mm hardcore. A ‘good’ subgrade with California bearing ratio (CBR) 15% (k = 60MN/m) and a ‘poor’ subgrade with CBR 3% (k = 27MN/m3) are considered.

ITN1 1 Tables 1-7 give slab thicknesses for various loadings. In TR34/3, Section 9.9 gives load capacity based on bending, 8.8 and 9.10 discuss load transfer at joints, 9.11 covers punching shear and there is a worked example in Appendix E2 (E2 has an error: the average effective depth of a 175mm-thick slab with A142 fabric at 50mm cover is not 125mm - it is 175-50-7 = 118mm).

Several points are worth noting:

* In T34/3, variations in subgrade quality do not affect load capacity.

* On a ‘poor’ subgrade, a 170mm slab would be required by TR550/ITN11 but only 129mm by TR34/3.

* In TR550/ITN11, the slab fails in bending but in TR34/3 it fails in shear (curiously, despite this, TR34/3 devotes seven pages to bending analysis and only one page to shear).

* Based on TR34/3 moment analysis, a slab on a poor subgrade would only need to be 99mm thick.

* After permitted construction tolerances (slab level ± 15mm, sub-base level +0/-25mm) a ‘129mm’ slab maybe only 114mm thick.

Analysis

When a new design method gives radically different results from past practice, it should be checked carefully. TR34/3 introduces three major changes:

* bending strength is calculated from plastic theory instead of elastic theory

* assumed load transfer at joints is increased

* slab load capacity is assumed to be the same at a joint intersection as at a single joint.

Table 2 compares allowable working loads (kN) based on bending analysis for a 150mm-thick slab with A142 mesh (150mm hardcore, subgrade CBR 3%, 40MPa cube strength, 100mm x 100mm racking leg base, tyre contact pressure 1.7MPa). Compared with TR550, TR34/3 permits three to four times as much load on a solid slab and about twice as much at a slab edge.

TR550 allows 15% load transfer at a single joint and 30% at a joint intersection. Two sections of TR34/3 discuss load transfer. According to 8.8.2 (p.45) friction provides 15% load transfer and steel fabric ‘typically provides 10% load transfer’. However according to 9.10, A142 mesh transfers 13.4kN/m (ultimate) over a length of 0.9 x l each side of the load (‘l’ is the radius of relative stiffness) subject to a total load transfer limit of 50% (A193 fabric transfers 18.3kN/m and A252 23.8kN/m).

Consider a 90kN forklift wheel (factored load 144kN) on a slab with ‘radius of effective stiffness’ of 700mm. According to TR34/3, load transfer at a joint would amount to 15% = 21.6kN (friction) plus 1.8 x 0.7 x 13.4kN/m = 16.9kN (fabric) = 38.5kN total (27%). However, with a 30kN forklift wheel (48kN factored), load transfer would be 7.2kN (friction) plus 16.9kN (fabric) = 24.1kN total (50%).

Thus TR34/3: a) increases load capacity in bending beside a joint; b) increases assumed load transfer at a joint; and c) says joint intersections can be ignored (8.8.2). The effect of combining these is a dramatic increase in the load that can be applied to a slab.

Analysis - load transfer at joints

TR34/3 assumes that dowel capacity at a joint is always fully mobilised, up to the total load transfer limit of 50% (9.10.1). Is this correct?

TR34/3 Appendix E

TR34/3 section 9.10 gives recommendations for load transfer at joints, based on bending analysis but it says nothing about how it should be calculated when punching shear is being considered. In the Appendix E2 worked example, the load transfer length is taken straight from 9.10, without any modification for the size of the punching shear perimeter. As a result, load transfer is overestimated and punching shear stress is underestimated.

In the example, 100mm square racking legs at 250mm c/c (combined factored load 144kN are positioned 70mm from a joint. The final slab design has d = 135, a punching shear perimeter of 1475mm and a shear capacity of 103.3kN. Load transfer is assumed across a length of 0.9 x I of joint to each side of the loads: total length 2 x 670 + 250 = 1590mm. Calculated load transfer (15% friction plus reinforcement dowel capacity) = 0.15 x 144 + 1.59 x 13.4 = 21.6 + 21.3 = 42.9kN. Thus net shear = 144 - 42.9 = 101.1kN, compared with capacity of 103.3kN.

However, load transfer outside the shear perimeter cannot reduce shear inside the perimeter (see Figure 1). The E2 calculation should only have considered the length of joint inside the shear perimeter: 350 + 540 = 890mm. Reducing load transfer pro rata for this reduced length gives a corrected value of 890/1590 x 42.9 = 24kN and the net shear becomes 144-24 24 = 1201(N. Instead of being ‘satisfactory’, the slab is actually 16% overstressed.

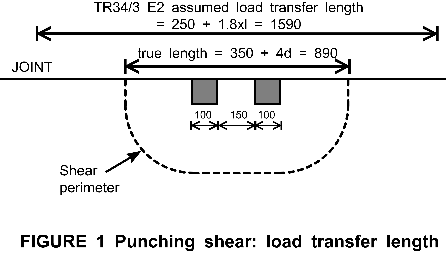
Limits on load transfer - bending

TR34/3 9.10 assumes that (within its overall 50% limit) load transfer at a joint depends on the friction that can be developed and the dowel strength of the reinforcement. However, other potential limiting factors have not been considered.

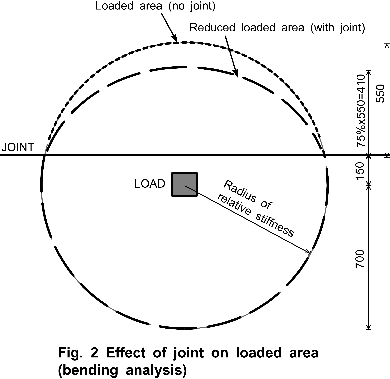
Consider a slab supporting a point load (Figure 2). If the ‘radius of relative stiffness’ defines the area supporting the load, then if l = 700mm, the area is it Π x 0.70²= 1.54m². If a joint is cut 150mm from the load, then 0.98m² of load- bearing area is on the ‘load’ side of the joint and 0.56m² (36%) on the other side. However, the loss of moment continuity at the joint will reduce load transfer across the joint, reducing the effective area on the other side to say 0.75% of 0.56m² = 0.42m² = 30% of the total area. Bearing pressure reduces towards the edges of the loaded area, so maximum load transfer across the joint is probably about 25%.

Limits on load transfer - shear

In punching shear calculations, the load transferred across a joint cannot exceed the strength of the slab on the other side.

Figure 3 shows a slab with an effective depth of 100mm supporting a 100mm x 100mm load centred 150mm from a joint. The length of the punching shear perimeter = 400 + 1256= 1,656mm, of which 100 +418 = 518mm is on the other side of the joint. If the joint was perfectly rigid, maximum load transfer would be 31%. A real joint will have some flexibility, so it will transfer less.

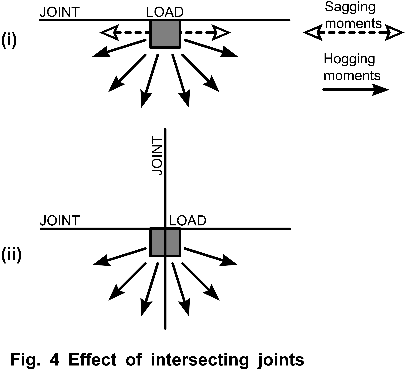
Joint intersections

Many engineers will be surprised by TR34/3 8.8.1: ‘Although the theoretical load capacity at the intersection of two joints is much lower than at a single joint, experience has shown that the actual capacity appears to be as great, given the same conditions of joint opening and provision of dowels or other load-transfer mechanisms’.

This is simply asserted, without any supporting evidence or references. The design method in this edition of TR34 is new and produces thinner slabs than past UK practice, so how can the claim in 8.8.1 be based on ‘experience’?

A load alongside a slab joint (Figure 4) is supported by sagging moments parallel to the slab edge and hogging moments radiating outwards from the load. What happens if another joint is cut in the slab at right angles to the first? The sagging moments and the load capacity they generate will be cut to zero, so the slab will be able to support less load. TR34/3 8.8.1 cannot be correct.

Concluding remarks

The TR34/3 recommendations for fabric-reinforced slabs have a number of errors:

* in a punching shear calculation, load transfer outside the shear perimeter should not be included

* consideration of loaded areas shows that maximum load transfer across a joint is about 25%, not 50%

* slab load capacity at a joint intersection is not equal to the capacity at a single joint.

In addition:

* research is needed to confirm whether fabric-reinforced ground-bearing slabs fail in shear or bending

* design safety factors should be reviewed taking into account the effect of construction tolerances on thin slabs.

References:

1. CONCRETE SOCIETY. Concrete Industrial Ground Floors: A Guide to design and construction. Technical Report 34, 3rd Edition, The Concrete Society, Camberley, 2003.

2.  DEACON, R.C. Concrete Ground Floors: their design, construction and finish. 3rd Edition, MPA Cement, Camberley, 1986 and 1987.

3.  CHANDLER, J.W.E. Design of Floors on Ground. Technical Report 550, MPA Cement, Camberley, 1982.

4.  CHANDLER, J.W.E. and NEAL, F.R. The Design of Concrete Ground-Supported Concrete Industrial Floor Slabs. Interim Technical Note 11, MPA Cement, Camberley, April 1988.

<< Return to top